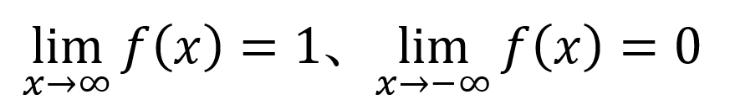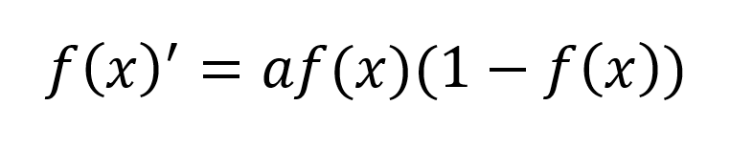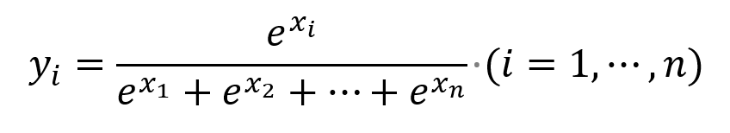シグモイド関数とは？ニューラルネットワークで用いられる理由についても解説

シグモイド関数は、ニューラルネットワークの活性化関数でよく用いられています。しかし、なぜシグモイド関数を用いるのか、どのような利点があるのか、ご存じない方もいるでしょう。

本記事ではシグモイド関数の式やおもな特徴、ニューラルネットワークで活用される理由を説明します。またシグモイド関数の代わりとなる関数についても合わせて紹介しましょう。

シグモイド関数とは

初めにシグモイド関数を表す数式やグラフ、関数の特徴について説明します。またステップ関数の近似に用いられることが多く、その理由について紹介します。

数式とグラフ

シグモイド関数はネイピア数eを用いた次の数式およびグラフで表されます。

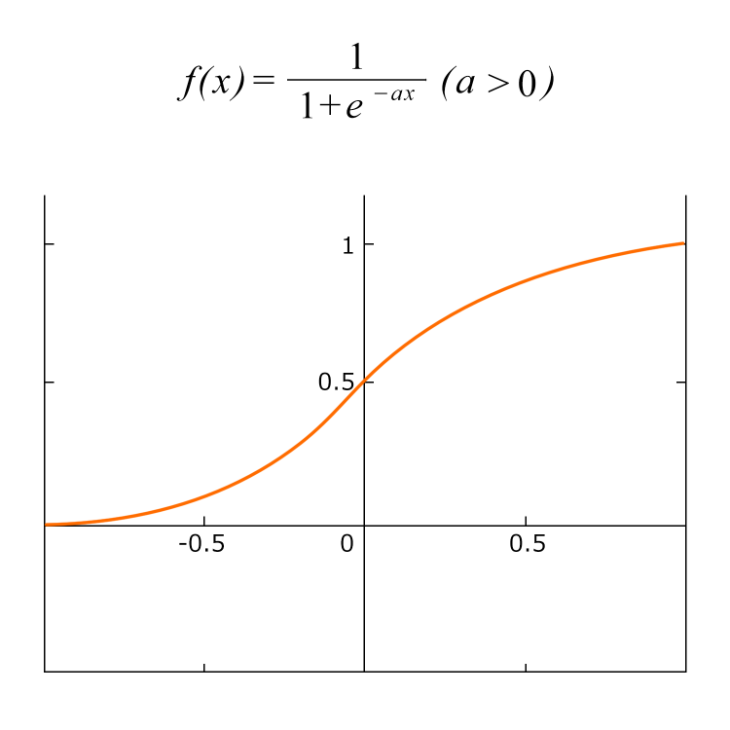
この関数は入力値xの値に依らず、0～1の数値に変換して出力します。グラフで表すとx=0の付近でf(x)は0から1へなだらかに増加。aの値によってグラフの傾きが変わり、値が大きいほど急激なカーブに、値が0に近いほどカーブがなだらかになるよう変化します。

グラフから読み取れるシグモイド関数の特徴をまとめると、以下のようになります。

・f(x)は単調増加する

・x=0のとき、f(x)=0.5となる

クリックして拡大

・(x, y)=(0, 0.5)に対して点対称なグラフとなる

4つ目の項目について補足すると、グラフの形状はS字型曲線を描いています。Sはギリシャ文字のσ(シグマ)に由来することから、この関数は「シグモイド関数」と呼ばれるようになりました。

シグモイド関数の一番の特徴は、関数を微分した姿にあります。微分形は以下の式のように元の関数f(x)を使って書き表せるため、簡易な計算で求められます。

クリックして拡大

本記事でも言及しますが、微分計算を活用できる用途として機械やロボットなどのシミュレーション、機械学習などがあります。そして微分計算が容易で、計算量を減らせることには大きなメリットも。例えば、シミュレーション速度の高速化、機械学習のパターン認識における精度の向上などを実現します。

ステップ関数の近似に用いられる

微分可能かつ微分計算が容易であるというメリットがあることから、シグモイド関数は他の関数の近似に用いられています。近似する関数の一例としてステップ関数について説明しましょう。

ステップ関数を式とグラフで表すと次のようになります。x=0のタイミングでf(x)が0から1へジャンプする階段状の波形であることから、ステップ関数と呼ばれています。ある特定のタイミングでスイッチをオンして、0から1に変化した状況などがイメージしやすいでしょう。

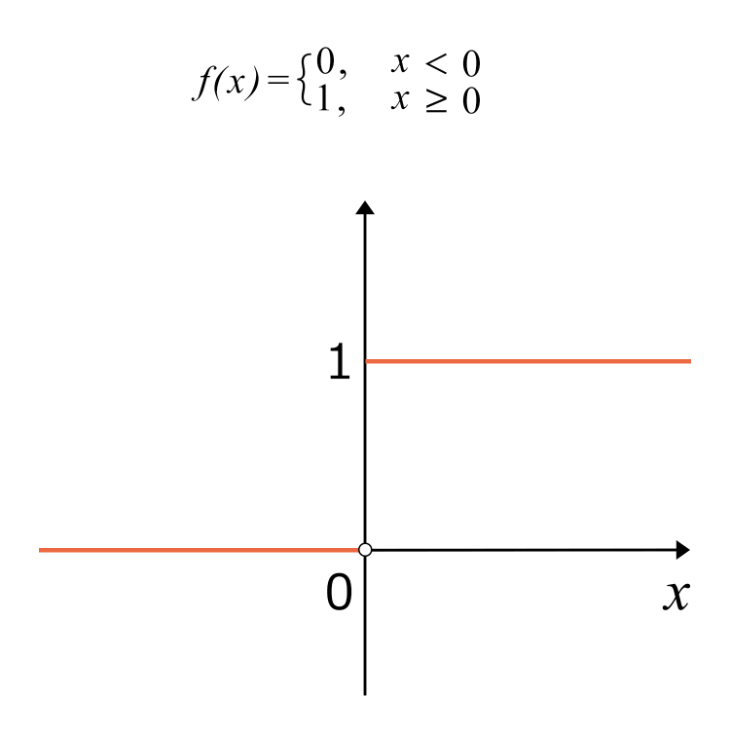
ステップ関数は制御工学の分野でよく用いられる関数です。制御工学とは機械やロボットなどのシステムに対し、ある目的を達成するような制御方式を設計する学問。例えばロボットに位置や速度の値を入力して、期待する動作をするか、安定した動作をするか、といった制御性能を満たすような設計を行ないます。

システムの入力値にステップ関数を用いた際の応答を、ステップ応答と呼びます。システムに一定値を入力し続けたときのシステムの振る舞いを検証する際に用います。しかしステップ関数はx=0付近で不連続なため微分計算ができないことが問題となります。そこでステップ関数と形状が似ており、微分可能なシグモイド関数で近似すると、システムを微分方程式として分析できるようになります。

機械やロボットなどのシステムだけでなく、あらゆる自然現象は「変化量」で表せます。そして変化量（＝微分量）を式で表したものが微分方程式。そのためシグモイド関数によりシステムを微分方程式で表現すると、システムに対しての考察をより深められます。

シグモイド関数と機械学習

シグモイド関数は機械学習の計算で多く活用されています。機械学習のどの部分で使用されているのか、シグモイド関数を使用するメリットとデメリットなどについて解説しましょう。

ニューラルネットワークの活性化関数

機械学習技術の一つであるニューラルネットワーク（以下、NN）とは、動物の脳内にある神経細胞（ニューロン）のネットワークを模擬したモデルのこと。大量のデータをモデルに入力し、データ内に含まれる要素の特徴を分析できることが特徴です。特にテキスト翻訳や音声認識などのパターン認識が必要な分野に向いています。他にもデータ分類や未来予測などにも活用され、入力データが多いほど精度の高い結果が得られる傾向にあります。

NNは相互に接続した複数のニューロンで構築された多層構造です。実際の脳内のニューロンの場合、「活性化」することで電気信号を別のニューロンへ伝播させ、情報を伝えています。脳を模擬したNNの場合、活性化関数を用いて活性化の挙動を表現します。使用する関数にはさまざまな種類があり、シグモイド関数もその一つ。関数の特徴の違いによりモデルとしての表現力が変わり、学習速度や精度にも影響します。

NNの課題は実際の出力と理想的な出力との差を埋めるモデルを作成すること。ニューロンの活性化により情報を伝えながらデータの学習を行なうため、ニューロンの層が深くなるほどモデルの表現力が向上します。ディープラーニング（深層学習）と呼ばれるネットワークではニューロンの層が数百層になることも。ニューロンの学習精度を向上させるため、日々研究が積み重ねられています。

シグモイド関数をニューラルネットワークで使用する際のメリットとデメリット

シグモイド関数は微分形を求める計算が容易であるため、NNの逆誤差伝搬法（バックプロパゲ―ション）に活用できることがメリットです。逆誤差伝搬法とは、モデルの理想的な出力と実際の出力との誤差を入力側の層に伝えることで、モデルのパラメータを決定するアルゴリズム。層数の多いNNで用いられる代表的な計算手法です。

一方、シグモイド関数を使用する際のデメリットは、「勾配消失」という現象のために逆誤差伝搬法の学習効果が限定的であること。各ニューロンのパラメータを更新してモデルの精度を高めるには、そのパラメータより先のニューロンを表す関数の偏微分である、「勾配」をかけ合わせる必要があります。

層数が多いNNでは、非線形変換を行なうたびに勾配が0.25倍されるため、次第に勾配が0に近づきます。すると入力層に近いパラメータの更新ができなくなり、学習が行なわれていない状態に。この問題のため、近年ではシグモイド関数はあまり使われなくなりました。

他の活性化関数の特徴

現在ではシグモイド関数の代わりに別の関数を用いることで、より深いNNのモデルを作成できるようになりました。いくつか例をご紹介しましょう。

ReLU関数

ReLU（Rectified Linear Unit）関数は次の式とグラフで表されます。またグラフの形状が斜面(ramp)のように見えることから、ランプ関数とも呼ばれています。

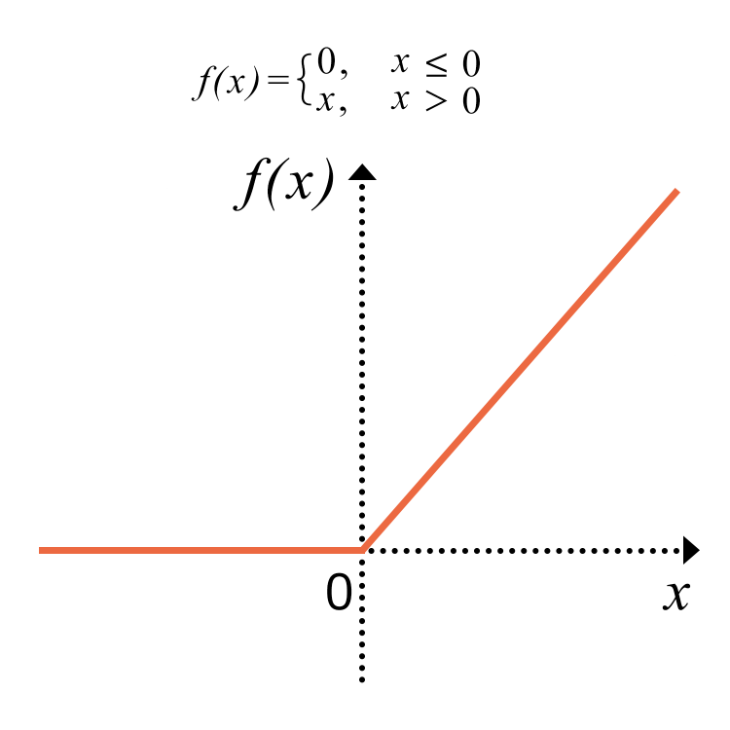
ReLU関数の特徴は勾配の最大値が1であること。そのため勾配消失の問題が改善できるというメリットがあります。また計算式がシンプルで、微分すると定数になることから、計算処理も高速に。そのためReLU関数はNNのモデルの活性化関数として、一般的に用いられています。

ただしグラフを見るとわかるように、ReLU関数はx=0の原点で不連続なために微分値が不定となってしまいます。またxが負の領域では値が0となるため機能しません。これらの特徴がモデルの学習の妨げになってしまうため、処理時間が長大化する、十分な学習が行なわれない、などの恐れもあります。

そのためReLU関数に新たなパラメータを導入して微分可能にする、xが負の領域を拡張するなど、さらに発展した形の関数も生み出されています。ReLU関数が発表されたのは2011年であり、現在までの間に数多くの関数が登場してきました。特に代表的なのが「Swish関数」、「Mish関数」であり、ReLU関数よりも高い精度を示しています。

ソフトマックス関数

ソフトマックス関数とは各出力成分が0より大きく、合計が1となる関数のこと。複数の実数の入力と出力を持ち、式で表すと次のようになります。

クリックして拡大

ちなみにi=2の場合は、式変形するとシグモイド関数になります。シグモイド関数の拡張版とも考えられるでしょう。

ソフトマックス関数の出力は0から1の値を取り、合計が1となることから、確率分布を表すためによく使用されています。実際にはNNの最終層として使用され、特に分類問題で効果を発揮します。

例えば、ある動物を写した画像をモデルに入力し、その動物が何かを当てるという分類問題を考えてみましょう。NNのモデルにソフトマックス関数を用いると、「犬の確率74％、猫の確率23％、ハムスターの確率3％」など、わかりやすい形で出力されます。ソフトマックス関数を使用しなければ、各出力の値を出力の合計値で割り算する計算処理などを追加する必要がありますが、この場合マイナスの値などを考慮する必要があります。

シグモイド関数はニューラルネットワークなどでも活用されている

シグモイド関数は入力値xを0～1の数値で出力する関数です。微分可能であること、微分形を簡単な計算で求められることが特徴で、制御工学で用いるステップ関数の代わりとしても利用できます。ま

たニューラルネットワークの分野では活性化関数としても活用。しかし、層数の多いモデルでは不向きであることがわかっています。近年では代わりにReLU関数およびその発展形の関数、ソフトマックス関数などが利用されています。