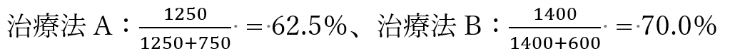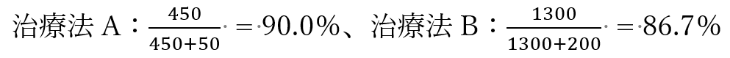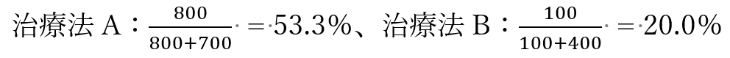シンプソンのパラドックスとは? おもな事例とデータの読み間違いを防ぐ方法について
統計データを扱う際に注意するべき「シンプソンのパラドックス」について紹介します。シンプソンのパラドックスにより、同じデータでも分析の仕方によって異なる結論が導かれてしまう恐れも。本記事ではシンプソンのパラドックスの概要と、パラドックスを見抜いてデータの読み間違いを防ぐ方法について紹介します。

統計データを扱う際に注意するべき「シンプソンのパラドックス」について紹介します。シンプソンのパラドックスにより、同じデータでも分析の仕方によって異なる結論が導かれてしまう恐れも。本記事ではシンプソンのパラドックスの概要と、パラドックスを見抜いてデータの読み間違いを防ぐ方法について紹介します。
知識・情報
2022/04/21 UP
- 技術
- おもしろ
統計データを扱う際に注意するべき「シンプソンのパラドックス」について紹介します。シンプソンのパラドックスにより、同じデータでも分析の仕方によって異なる結論が導かれてしまう恐れも。本記事ではシンプソンのパラドックスの概要と、パラドックスを見抜いてデータの読み間違いを防ぐ方法について紹介します。

シンプソンのパラドックスとは
「データの母集団全体における相関と、その母集団を分割した一部の集団における相関は必ずしも一致しない」ことを、シンプソンのパラドックスと呼びます。1951年にイギリスの統計学者シンプソンが発表した論文で登場したため、この呼び名が使われるようになりました。大量のデータで構成された統計データを扱う際に注意すべきパラドックスです。
大量の数値データを使って説明されると、人はその説明が論理的で正しいと判断しがちです。しかし、数学的には矛盾していないのにも関わらず、データの抽出の仕方によってはデータと矛盾した主観的な結論を導いてしまうこともあります。データ分析で起こりがちな、この思い違いを明らかにするのがシンプソンのパラドックスです。
私たちが普段の生活で目にするデータにもシンプソンのパラドックスは潜んでいます。また近年ではビッグデータやAIの発展とともに、業務などで統計データを扱う機会が増えている人も多いでしょう。パラドックスについて理解を深めることが、データの読み間違いを防ぐことにつながります。
なぜパラドックスが生じるのか

シンプソンのパラドックスとはどういうものか、具体例を使って説明しましょう。また、なぜデータと矛盾した結論を導いてしまうのか、その理由も解説します。
2つの治療法の効果の例
ある病気に対して、2つの治療法AとBが存在します。どちらの治療法の効果が高いか確認するため、男女それぞれ2000人ずつの被験者に試して効果を確認することにしました。その結果をまとめたのが次の表です。
| 治療法 | A | B | ||
|---|---|---|---|---|
| 治療の効果 | あり | なし | あり | なし |
| 男性 | 450 | 50 | 1300 | 200 |
| 女性 | 800 | 700 | 100 | 400 |
| 合計 | 1250 | 750 | 1400 | 600 |
男女の合計の結果について、治療法AとBそれぞれで効果ありとなった割合を計算しましょう。すると以下の結果が得られ、治療法Bのほうが有効だと考えられます。
次に、男女別で治療法AとBそれぞれで効果ありとなった割合を計算しましょう。すると先ほどの結果とは違った印象になります。
男性の場合
女性の場合
今度は男性も女性も治療法Aのほうが有効です。男女を合計した場合は治療法Bのほうが有効なのに、男女別の場合は治療法Aのほうが有効という、一見矛盾するような結果が得られました。
これこそが母集団(男女合計のデータ)と、その母集団を分割した集団(男性のみ、女性のみのデータ)で相関が異なるという、シンプソンのパラドックスです。
パラドックスが生じる理由
治療法AとBの計算例では奇妙な現象が得られましたが、数学的な観点から解析すると矛盾がないことがわかります。先ほどは具体的な数字で割合を比較しましたが、今度は文字に置き換えて比較しましょう。男女別における、各治療法での効果があった割合の比較は、次の2式で表します。
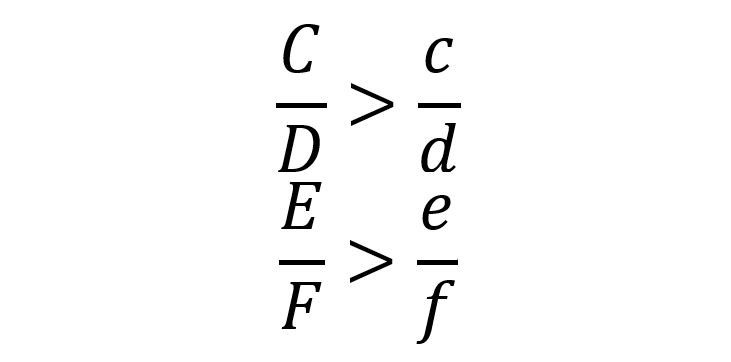
ここで重要なことは、たとえ上の2式が成り立つ場合でも、各分子と分母を合計した次の式が成り立つとは限らないということです。反対に、下の式が成り立つ場合でも上の2式が成り立つとは限りません。
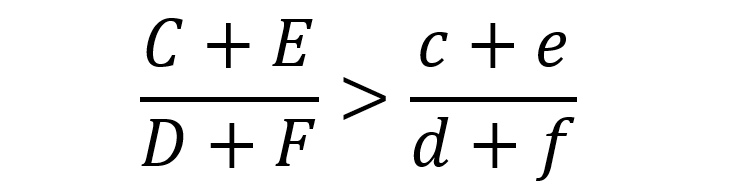
つまり数学的には成り立たないことが明らかな現象であるのに、データの数字を見せられると間違って解釈してしまうのです。
パラドックスが起こってしまった原因は、治療法と効果の因果関係を見誤ったためです。治療法と効果それぞれに影響する「性別」という要因を考慮するか否かで、結果が変わってしまいました。詳細は後述しますが、原因と結果の両方に影響する要因を「交絡要因」と呼びます
データに潜むパラドックスの例
シンプソンのパラドックスに関して他の例を考えてみましょう。私たちが普段目にするようなデータのなかにもシンプソンのパラドックスが潜んでいます。
大学の就職率
A大学とB大学にはそれぞれ1000人の学生が在籍しています。各大学が公表した就職率を表にまとめると以下のようになりました。
| 理系 | 文系 | 全学生 | |
|---|---|---|---|
| A大学 | 79% (632人/800人) | 58% (116人/200人) | 75% (1000人) |
| B大学 | 88% (132人/150人) | 71% (600人/850人) | 73% (1000人) |
2大学を全学生の結果で比較すると、A大学のほうが高い就職率であることがわかります。一方で理系と文系それぞれで比較すると、就職率が高いのはどちらもB大学。集団全体に注目するか、分割した集団に注目するかで結果が異なるという、シンプソンのパラドックスが起きています。
A大学とB大学の就職率を文理で比較すると、どちらも理系のほうが高い傾向にあるため、理系学生のほうが就職しやすい景気であったとも考えられます。するとA大学のほうが理系の学生数が多いことが影響して、全学生における比較ではA大学が勝る結果となったと予想できます。
今回の例では理系と文系の就職率のデータが存在するため、文理それぞれの比較ができました。しかし、もし全学生のみのデータしか無ければ、A大学のほうが高い就職率を誇る大学だと信じてしまったのではないでしょうか。
データをどう切り取るかというのは、データを提供する側の判断に依ることもあります。十分なデータが得られなかったために、大学選びのような重要な判断を間違えてしまうかもしれません。
平均所得の変化
高所得者と低所得者それぞれのグループの平均所得は上昇しているのに、全体の平均所得は減少している。このようなニュースを見たとしたら、違和感を覚える人は多いのではないでしょうか。しかし、これは現実に起こりうることです。
A氏、B氏、C氏、D氏、E氏の5人の所得金額を昨年と今年とで比較し、高所得者と低所得者にグループ分けします。まず5人の所得金額をまとめると以下の表のようになりました。
| 昨年の所得金額[万円] | 今年の所得金額[万円] | |
|---|---|---|
| A氏 | 2000 | 1800 |
| B氏 | 1200 | 950 |
| C氏 | 720 | 680 |
| D氏 | 600 | 580 |
| E氏 | 420 | 380 |
次に高所得者と低所得者という2グループに分け、各グループおよび全体の平均金額を算出しました。なお1000万円以上を高所得者、1000万円未満を低所得者としています。
| 昨年の平均所得 [万円] | 今年の平均所得[万円] | |
|---|---|---|
| 高所得者 | 1600 | 1800 |
| 低所得者 | 580 | 648 |
| 全体 | 988 | 878 |
表を見ると、高所得者のグループと低所得者のグループはどちらも昨年より所得が増加しました。しかし全体では昨年よりも所得が下がる結果に。なぜこのような現象が起きたのでしょうか。
原因はB氏の所得が1200万円から950万円に下がり、B氏が高所得者のグループから低所得者のグループへ移動したためです。B氏はもともと高所得者層にいたため、低所得者層のグループに入った際にも1000万円近い所得があることから、グループの平均所得を引き上げてしまいました。
一方で高所得者のグループは、B氏が抜けて所得が高いA氏のみになったことで平均所得が増える結果に。このように昨年と今年とでグループを移動した人がいるとわかれば、おかしな結果ではありません。
シンプソンのパラドックスを見抜くために

シンプソンのパラドックスに引っかからないようにするには、何ができるでしょうか。データの読み間違いを防ぐために意識すべきことを紹介します。
正しい因果関係を把握すること
データから正しい因果関係を把握することが、データを読み間違えないための第一歩です。記事の最初に紹介した治療法の例では、「効果があった人の割合が高い」と数学的に考えれば矛盾はありません。しかし被験者全体で見て効果があるなら、男女別に分けても同じく効果があるはず、という解釈には因果関係がなく、誤った判断となるため注意してください。
原因と結果による因果関係を統計的に推定することを、因果推論と呼びます。治療法の例のように、与えられたデータに対して勝手に因果関係を想像して解釈してしまい、因果推論を誤ったことがパラドックスの原因です。
隠れた交絡因子を見つけ出すこと
シンプソンのパラドックスで因果関係を見誤ってしまう原因は「交絡因子」にあります。交絡因子とは、ある因果関係における原因と関連し、結果に影響を与えるような要因のこと。交絡因子の存在に気付けば、データの読み間違いを防げます。
治療法の例における交絡因子は「性別」です。AとBの治療法のどちらを選んだかという原因について、男女で差があります。例えば性別によって治療の可否が異なる可能性があります。また女性のほうが病気のリスクが高く、治療法が効きにくいのかもしれません。因果関係に影響を与える要素に関連した切り口を見つけられれば、データを正しく判断できます。
実際のデータを扱う際には、データが不十分で交絡因子がはっきりと見えない場合もあるでしょう。また交絡因子が1つではなく、複数が相互に影響しあっており解析が困難となることも考えられます。それでもデータのなかに潜む交絡因子は何か、という観点を忘れないよう意識することが大切です。
身近なデータの中にもシンプソンのパラドックスは潜んでいる
データ全体における相関と、分割した一部のデータ内における相関は必ずしも一致しないことを、シンプソンのパラドックスと呼びます。大学の就職率や平均所得の変化など、私たちの身近なデータのなかにもパラドックスは潜んでいます。
パラドックスが起こるのは原因と結果の双方に影響を与える交絡因子の存在によるもの。データを読み取る際には正しい因果関係を把握することと、隠れた交絡因子を見つけ出すことに注意してください。